为什么钢筋放太多了反而不好呢？  ,钢筋,in

转自知乎 （原作者：猪小宝），谢谢原作者的详细剖析。

    一根混凝土简支梁，跨中蒙受集中荷载。我们假设简支梁的跨度是200英寸，截面高度是18英寸，截面宽度是16英寸。排除其它条件的滋扰，我们接纳单筋截面，钢筋中心线到受压边沿的距离d 也相同，取为15.5英寸。混凝土强度 4 ksi，钢筋强度 60 ksi。

    为了比较梁受弯承载力随钢筋面积的转变，我们考虑四种情况，钢筋面积分别为2平方英寸、4平方英寸、6平方英寸、8平方英寸。实际配筋面积不太可能全是这样的整数，我们只是为了计算和比较方便。

    首先，我们明确一点。什么叫破坏？钢筋混凝土梁破坏，即是混凝土压应变到达极限压应变。ACI 规范里极限压应变是0.003，中国规范是0.0033，我们在下面的例子里接纳0.003。

第一阶段：开始加载到混凝土开裂

    我们逐渐加载，到某一个临界点，受拉侧的混凝土开裂。这一临界点我们用 cr（cracking）体现。

    剖析也很简单，大众都市，凭据弹性模量的比例把钢筋换算为等价的混凝土面积。此时，钢筋混凝土截面酿成了均一质料组成的截面，相符质料力学的种种简化理论。

    混凝土开裂的准则是混凝土拉应力到达开裂应力 fr。对付同一种强度品级的混凝土，fr 是一个定值，可以近似用

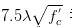
来计算。所以，混凝土的开裂拉应变也是一个定值，即是这个开裂应力除以弹性模量，

。对付强度 4 ksi 的混凝土来说，这个开裂拉应变即是0.0001316。

    对付我们这四种差别配筋的截面，开裂剖析结果如下：

• 钢筋面积 2 in^2，中性轴距截面上侧的距离 c=9.303 in，开裂弯矩 455.069 k-in，开裂曲率15.129*10^-6 rad/in，混凝土压应变 0.0001408
• 钢筋面积 4 in^2，中性轴距截面上侧的距离 c=9.579 in，开裂弯矩 499.109 k-in，开裂曲率15.626*10^-6 rad/in，混凝土压应变 0.0001497
• 钢筋面积 6 in^2，中性轴距截面上侧的距离 c=9.832 in，开裂弯矩 541.999 k-in，开裂曲率16.109*10^-6 rad/in，混凝土压应变 0.0001584
• 钢筋面积 8 in^2，中性轴距截面上侧的距离 c=10.064 in，开裂弯矩 583.784 k-in，开裂曲率16.579*10^-6 rad/in，混凝土压应变 0.0001669

    看，混凝土开裂的时候，混凝土压应变只有 0.00015 左右，离 0.003 还远着呢。所以，钢筋混凝土在从 0.00015 到 0.003 的漫长余生里都是带裂缝劳动的。这也是大众常说的混凝土如果不开裂，钢筋基本不起作用。

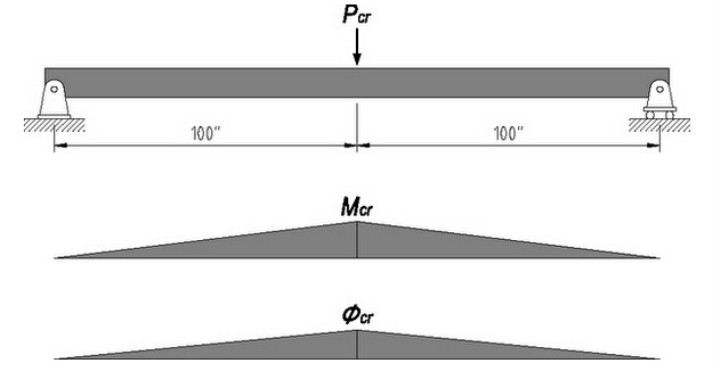
    对付这根简支梁，我们现在知道了跨中弯矩和跨中截面的曲率，问：能不克算出跨中集中力和跨中竖向位移？能不克？说不克的同学，请认真温习作业。

• 钢筋面积 2 in^2，混凝土开裂时的集中力 9.10 kip，跨中竖向位移 0.050 in
• 钢筋面积 4 in^2，混凝土开裂时的集中力 9.98 kip，跨中竖向位移 0.052 in
• 钢筋面积 6 in^2，混凝土开裂时的集中力 10.84 kip，跨中竖向位移 0.054 in
• 钢筋面积 8 in^2，混凝土开裂时的集中力 11.68 kip，跨中竖向位移 0.055 in

    从这个结果我们也能得到一个特别收获，那就是如果为了控制裂缝和挠度，加钢筋几乎是没有用的。从2平方英寸到8平方英寸，钢筋面积翻了两番，开裂时的挠度反而更大了。

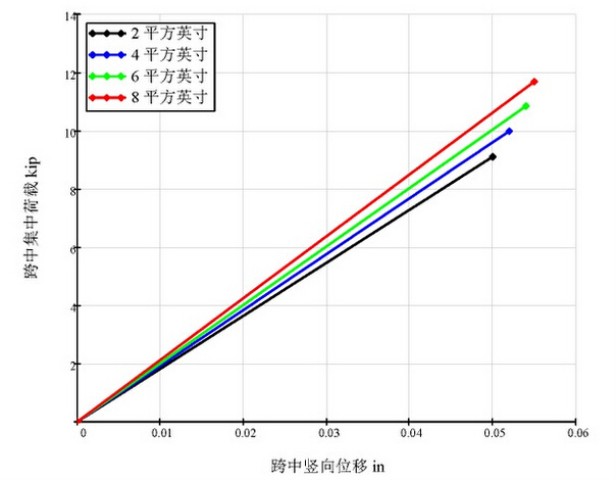
    这是集中力和竖向位移的图形，四根梁的颜色分别为黑色、蓝色、绿色和红色。虽然钢筋面积相差很大，但是，直到混凝土开裂之前，总体上没有大的区别。

第二阶段：混凝土开裂到钢筋屈服

    混凝土开裂之后，我们继续加载，此时混凝土裂缝逐渐向上成长，混凝土受压区变小。拉力从开裂掉的混凝土身上转移到钢筋身上，钢筋拉力逐渐加大。到某一个时刻，钢筋到达屈服强度。这一个临界点我们用 y（yielding） 体现。

    判断屈服极限点的准则就是钢筋到达屈服强度，因为我们用的是同一种钢筋，所以其实也就是钢筋到达屈服拉应变。也就是说，钢筋的屈服拉应变是一个定值，

。对付60 ksi 的钢筋来说，这个屈服拉应变即是0.002069。

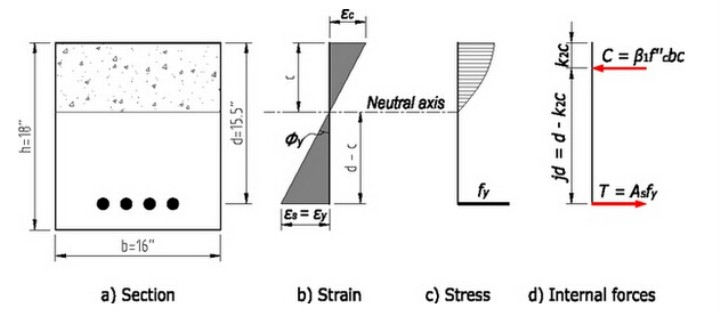
    为了包管结果的准确性，我们接纳较为准确的混凝土受压区的抛物线应力漫衍，而不是近似的三角形漫衍。

    对付我们这四种差别配筋的截面，屈服剖析结果如下：

• 钢筋面积 2 in^2，中性轴距截面上侧的距离 c=4.777 in，屈服弯矩 1660.746 k-in，屈服曲率192.947*10^-6 rad/in，混凝土压应变 0.0009217
• 钢筋面积 4 in^2，中性轴距截面上侧的距离 c=6.648 in，屈服弯矩 3132.414 k-in，屈服曲率233.729*10^-6 rad/in，混凝土压应变 0.001554
• 钢筋面积 6 in^2，中性轴距截面上侧的距离 c=8.293 in，屈服弯矩 4390.295 k-in，屈服曲率287.077*10^-6 rad/in，混凝土压应变 0.002381
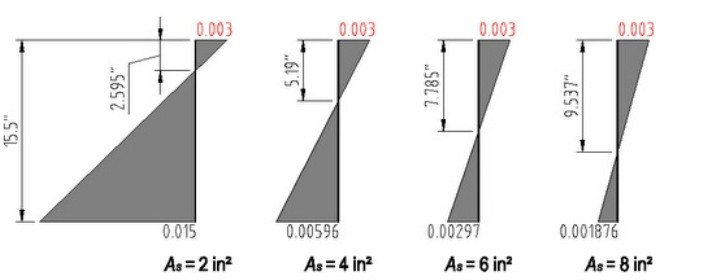
• 钢筋面积 8 in^2，如果凭据上面的计算过程，此时 c=10.395 in。但是，注意到，此时混凝土压应变已经到达了 0.004213，远远超出了 0.003。也就是说，这是根超筋梁，钢筋不可能屈服，混凝土会在钢筋屈服之前就到达0.003的极限压应变。我们反过去推算，已知混凝土压应变是0.003，求钢筋拉应变是几多？计算结果是此时 c=9.537 in，钢筋拉应变为0.001876，小于屈服拉应变0.002069。当混凝土压应变到达0.003时，弯矩为 5516.679 k-in，曲率为 346.967*10^-6 rad/in

    注意，下面这个屈服应变图跟上面的开裂应变图的比例差别，因为都按同一个比例的话，下面这张图就实在太宽了。

    当到达钢筋屈服点的时候：第一根梁，混凝土压应变还不到0.001，离着 0.003 的压碎点还有好长一段距离；第二根梁，压应变到达了0.0015，已经走完了 0.003 的一半；第三根梁，压应变 0.002381，人生路已经差未几了，快要到 0.003 的死亡点了；第四根梁，钢筋还没屈服呢，混凝土就压碎了，人死了，钱还没花完，你说这事儿闹的。

    同开裂一样，我们现在知道了屈服时的跨中弯矩和跨中截面的曲率，我们同样可以得出屈服时跨中集中力和跨中竖向位移。注意，因为混凝土开裂，所以，此时的混凝土梁相当于一根变刚度梁。

• 钢筋面积 2 in^2，钢筋屈服时的集中力 33.22 kip，跨中竖向位移 0.563 in
• 钢筋面积 4 in^2，钢筋屈服时的集中力 62.65 kip，跨中竖向位移 0.737 in
• 钢筋面积 6 in^2，钢筋屈服时的集中力 87.8 kip，跨中竖向位移 0.921 in
• 钢筋面积 8 in^2，混凝土应变到达 0.003 时的集中力 110.33 kip，跨中竖向位移 1.119 in

    这个结果报告我们什么呢？基本上，钢筋屈服时的承载力跟钢筋面积是成正比的。钢筋面积从2到4再到6，承载力分别为大抵30、60、90。注意到，第四根承载力不是120左右，而是只有110左右。那是因为它人死了，钱没花完，还有一局部钢筋没用完，所以没能到达120。

第三阶段：钢筋屈服到混凝土到达极限压应变

    很遗憾，第四根梁已经提前牺牲了，所以能走进这一阶段的只有前三根。

    钢筋屈服之后，我们继续加载，此时钢筋应力不会再增加，混凝土压应力逐渐增加，受压区高度逐渐减小，压应变逐渐变大，直至到达最终的死亡点——压应变 0.003。这个死亡临界点我们用 ult（ultimate）体现。

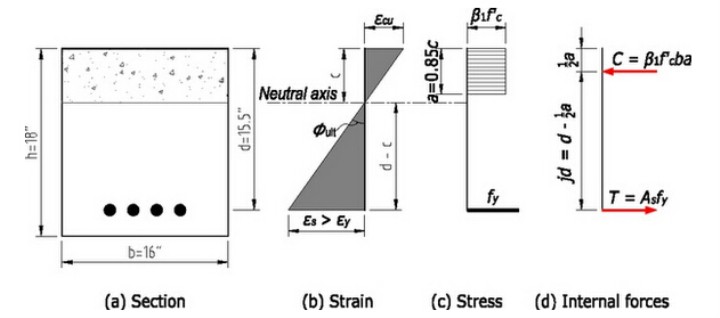
    死亡临界点的判断准则也很简单，我们也强调了好几次了，那就是混凝土压应变 0.003。在极限阶段，混凝土近似接纳矩形应力漫衍已经足够准确，所以我们也接纳矩形应力漫衍。

    对付我们剩下的这三根战斗到最后的梁，极限状态剖析结果如下：

• 钢筋面积 2 in^2，中性轴距截面上侧的距离 c=2.595 in，极限弯矩 1727.647 k-in，极限曲率1156*10^-6 rad/in，钢筋拉应变 0.015
• 钢筋面积 4 in^2，中性轴距截面上侧的距离 c=5.190 in，极限弯矩 3190.588 k-in，极限曲率578*10^-6 rad/in，钢筋拉应变 0.00596
• 钢筋面积 6 in^2，中性轴距截面上侧的距离 c=7.785 in，极限弯矩 4388.824 k-in，极限曲率385.333*10^-6 rad/in，钢筋拉应变 0.00297

    同样，我们继续反算跨中集中力和跨中竖向位移。此时，跨中完全屈服，守旧预计，我们近似将跨中的屈服范畴定为与d相同，即是 15.5 英寸。实际的屈服范畴完全可以比这个大得多，但我们只按最守旧的情况估算。

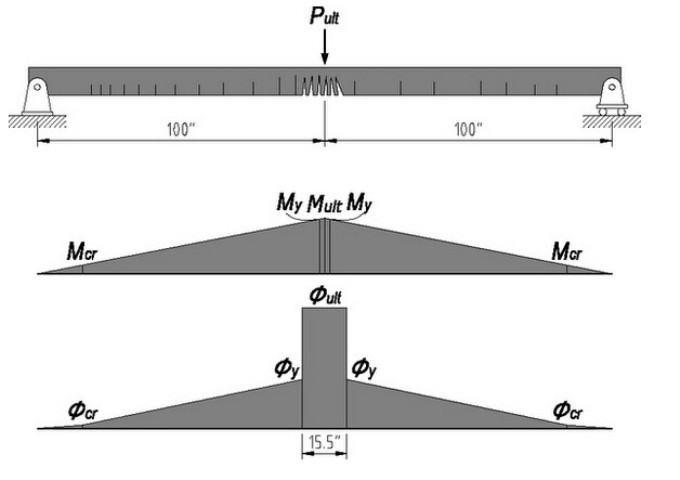
• 钢筋面积 2 in^2，最终破坏时的集中力 34.55 kip，跨中竖向位移 1.336 in
• 钢筋面积 4 in^2，最终破坏时的集中力 63.81 kip，跨中竖向位移 1.054 in
• 钢筋面积 6 in^2，最终破坏时的集中力 87.8 kip，跨中竖向位移 1.066 in

    跟上面屈服点的计算结果比拟一下，我们能得出什么结论呢？承载力几乎没有转变，还是大抵30、60、90，但是，位移全部变大了。增加最多的是第一根，从0.563 英寸大幅增大到了 1.336英寸；增加最少的是第三根，从0.921英寸小幅增大到 1.066英寸。
    下面，我们终于回到正题了。我们看一下上面这张 P-Δ 曲线，它能报告我们什么呢？

    首先，我们可以判断承载力。如果跨中集中荷载为 20 kip，那么钢筋 2 平方英寸的第一根梁就够了；如果外荷载为 60 kip，我们需要第二根梁；如果外荷载为80 kip，那么我们需要第三根梁；注意，如果外荷载为 100 kip，我们需要的不是第四根梁，我们需要的是一根截面更大的梁。

    其次，我们可以判断耗能情况。什么叫耗能？这张图横坐标是位移，纵坐标是外力。问：力乘以位移即是什么？答：即是能量。没错，每一条曲线下的面积就即是这根梁从开始加载到最终破坏所能消耗的所有能量。很多时候，外力不是以静力荷载的形式作用在结构上，而是以动能的形式，好比爆炸、地动、撞击等等。这个时候，耗能能力的比较就显得很重要了。

    那我们这四根梁的耗能能力如何呢？很简单的几何题，算曲线与横轴之间的面积，中学生都市。四根梁的耗能能力依次为 37.26 k-in、45.15 k-in、55.77 k-in、65.24 k-in。

    举个例子，好比这根梁位于产业建筑内，跨中上方有一个设备，由于种种原因，这个设备有可能会偶然掉下来，那会不会把这根梁砸坏呢？假设这个设备重30000磅，掉下来撞击到梁的瞬间速度为每秒3英尺，那总的动能就是，

    即是50.35k-in。这时候，就需要第三根梁了。虽然第二根梁的静力承载力超出了 60000 磅，但是依然经受不住 30000 磅重的东西每秒3英尺速度的撞击。

    第三，我们可以比较一下钢筋用量的提高带来的承载能力和耗能能力提高的效果。钢筋从2增加到6，钢筋放大了3倍，极限承载力从 34.55 放大到 87.8，放大了大抵2.5倍，而耗能能力从 37.26 增加到 55.77，只放大了不到1.5倍。第一根梁跟第四根梁比拟，钢筋放大了4倍，耗能只放大了1.75倍左右。并且，我们考虑的屈服范畴是凭据最守旧预计的，实际的耗能能力提高的倍数，只会更小。

    第四，我们可以比较一下最终破坏时的变形能力。很明显，配筋越多，破坏时的位移越小。或者，我们也可以通过弯矩-曲率曲线看到这一趋势。

    钢筋越多，弯矩-曲率曲线从屈服到破坏越短，极限曲率越小，说明梁截面的转动变形能力越小。基本上，对付适筋梁来说，极限曲率跟钢筋面积成反比。抗震设计，很多时候看中的就是耗能和变形能力。也就是说，在这种时候，盲目的放大钢筋并不是个好选择。

第五，准则值到设计值的折减造成的影响。以上讨论的全部是准则值，用于实际设计的话，用的是折减后的设计值。简单说，配筋越多，钢筋拉应变越小，折减的越厉害。

这是这梁的极限弯矩承载力与配筋量的关系。我们先看红色曲线，横坐标为2，纵坐标接近2000，横坐标4，纵坐标3000左右，横坐标6，纵坐标4500左右，相符我们上面的计算结果。

蓝色的 Mu 就是折减后的弯矩设计承载力。很明显，在配筋量大于5之后，几乎就是水平直线了。甚至因为配筋量加大，需要接纳双排钢筋，反而还有下降。所以，哪怕你不管耗能、变形能力，仅仅比较承载力，也不是钢筋越多越好。例子里的这根梁，配置5平方英寸以上的钢筋对承载力不会有任何提升。

其实呢，我罗罗嗦嗦这么多，解释的就是一个「延性」的观点。虽然可能超筋梁纸面上的承载力看上去也没什么问题，但是它已经不是一个延性混凝土构件了。没有延性，最大的问题就是变形能力严重不敷，耗能也不敷理想，很不相符「大震不倒」的设计准则。换言之，地动来了，结构变形非常大，这时候适筋梁处在它第三阶段的直线上，半断连续，苟延残喘，大众还能踩着它们逃命；而超筋梁呢，基础没有第三阶段的那段直线，很有可能「喀嚓」一声就彻底不可了，多的那些钢筋全是浪费，发挥不了什么作用。

所以呢，合理的抗震设计计谋就是制止超筋梁，用合理的结构安排、截面尺寸、钢筋配置换取最大的变形能力和耗能能力。盲目的多加钢筋，可能会适得其反。实际工程实践中，很多工程师喜欢盲目的放大钢筋，美其名曰追求安定性能，次梁用25的钢筋，框架梁全部28的。我觉得呢，追求安定没错，但是得科学合理，不克好心办坏事。就拿这个例子来说吧，如果设计荷载的集中力是25 kip，那你配个2平方英寸的钢筋就足够了。如果你非得用8平方英寸的钢筋，不但花了4倍的钱，还减少了差未几五分之一的最大变形能力，这是何苦呢？

我们在这里剖析的，只是钢筋面积的影响。如果我转变截面宽度呢？截面高度？我提高混凝土强度呢？提高钢筋强度呢？如果我配置受压钢筋呢？这些会对承载力、耗能、变形能力有什么影响呢？有兴趣的同学们，自己试试看吧。